论文标题:ICARUS: A Specialized Architecture for Neural Radiance Fields Rendering
论文来源:SIGGRAPH Asia 2022
论文作者:Chaolin Rao, Huangjie Yu, Haochuan Wan, Jindong Zhou, Yueyang Zheng, Yu Ma, Anpei Chen, Minye Wu, Binzhe Yuan, Pingqiang Zhou, Xin Lou, Jingyi Yu
简介
本篇文章介绍了 NeRF 硬件加速的实现。
NeRF 回顾
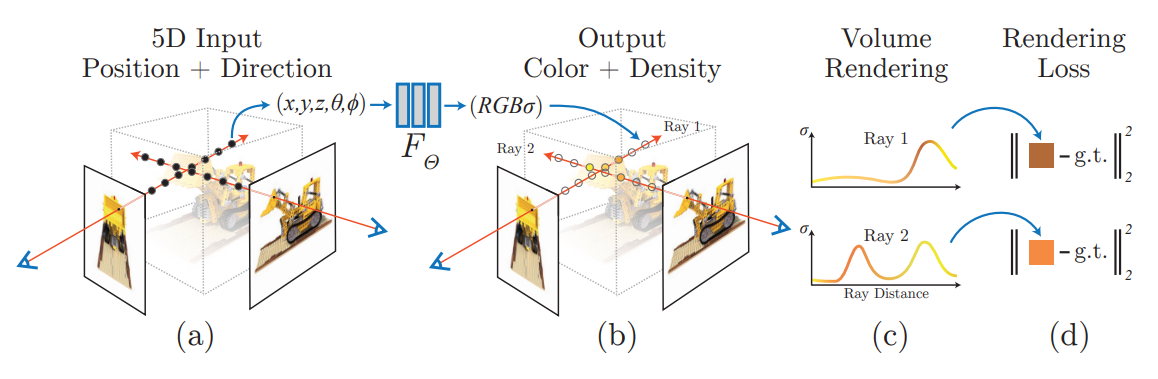
Neural Radiance Field,简称 NeRF,最开始在 ECCV 2020 上被提出,提出了以神经网络编码辐射场的一种技术,并且将其运用到了基于图片的场景重建等多个领域中,是近年来受关注度相当高的一篇工作。
NeRF 的网络部分输入为 5D: 位置 $ (x,y,z) $ 和朝向 $ (\theta, \phi) $,输出为该位置的 RGB 颜色和密度。
NeRF 在给定相机位置下最终渲染的输出用类似体渲染 (Volumetric Rendering) 的办法来实现。
NeRF 体渲染
对给定的相机光线 $ {\bf r}(t) = {\bf o} + t{\bf d} $ 来说,最终输出的颜色 $ {\bf C}(r) $ 以下式表示:
$$ C({\bf r}) = \int_{t_n}^{t_f} T(t) \sigma({\bf r}(t)) {\bf c}({\bf r}(t), {\bf d}) dt $$其中:
- $ T(t) = \exp (-\int_{t_n}^{t} \sigma({\bf r}(s)) ds ) $ 为光线从 $ t_n $ 能打到 $ t $ 的概率
- 比如说,如果射线穿过的部分密度都比较大,那 $ T(t) $ 就会比较小
- $ \sigma({\bf r}(t)) $ 是该 $ t $ 对应的点 $ {\bf r}(t) $ 的密度
- $ {\bf c}({\bf r}(t), {\bf d}) $ 是网络给定方向和位置后输出的 RGB 颜色值
- $ t_n $ 和 $ t_f $ 分别为射线进入和射出 NeRF 有效区域的包围盒时所对应的最近和最远参数值
不过这个积分显然不能很容易的解析求解,NeRF 的做法是采用数值积分的那一套。
首先,利用分层抽样 (stratified sampling) 的技术,将 $ [t_n, t_f] $ 分成 $ N $ 个均匀的小区间,然后在每个小区间均匀采样出一个 $ t_i $ 出来。
然后,用下面的量 $ \hat C({\bf r}) $ 来估计上面的 $ C({\bf r}) $:
$$ \hat C({\bf r}) = \sum_{i=1}^{N} T_i (1-\exp(-\sigma_i \delta_i)) {\bf c}_i $$其中:
- $ T_i = \exp(- \sum_{j=1}^{i-1} \sigma_j \delta_j) $
- $ \delta_i = t_{i+1} - t_i $ 为两临近采样点的距离
为什么会变成这个形式?可以参考 arXiv 上的 Volume Rendering Digest (for NeRF)
原文中提到,从所有的 $ ({\bf c}_i, \delta_i) $ 对考虑的话,$ \hat C(r) $ 的计算显然是可微的,并且可以看成从最开始一直用 $ \alpha_i = 1 - \exp(\sigma_i \delta_i) $ 的透明度往上面做 alpha blending。
NeRF 网络
网络部分用位置编码 (Positional Encoding) + Coarse MLP + Fine MLP。
位置编码
位置编码用来改善网络对高频细节的学习效果。
位置编码层可以如下描述:
$$ \gamma(p) = (\sin(2^0 \pi p), \cos(2^0 \pi p), ..., \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p)) $$Coarse & Fine MLP
NeRF 同时使用两个 MLP 来表示场景,一个粗粒度 MLP 和一个细粒度 MLP。
渲染的时候,首先用分层抽样的办法,在粗粒度网络中用前面提到的体渲染方法进行渲染,并且得到输出 $ \hat C_c(r) $:
$$ \hat C_c(r) = \sum_{i=1}^{N_c} w_i c_i, \quad w_i = T_i (1-\exp(\sigma_i \delta_i)) $$然后,计算归一化权重 $ \hat w_i = w_i / \sum_{i=1}^{N_c} w_i $,并且用计算好的归一化权重作为概率分布函数 (cumulative distribution function),再在这条直线上采样 $ N_f $ 个位置,将这 $ N_c + N_f $ 个位置送入细粒度 MLP 进行推理,再用前面的办法渲染得到最终的颜色值。
损失函数
采用简单的把 Coarse MLP 和 Fine MLP 与真实值之间的 $ L^2 $ 损失直接加起来的办法。
ICARUS
NeRF 计算过程回顾
- 对像素所发出射线上的采样,得到点 $ ({\bf p}_1, …, {\bf p}_N) $
- 查询 MLP 网络:$ ({\bf p}_i, {\bf d}_i) \to ({\bf c_i}, \sigma_i) $
- 进行多次 alpha-blending
架构设计
架构设计时主要有以下目标:
- “端到端” - 芯片输入位置和方向,输出像素颜色,减少片上片外数据交换的额外开销(计算时间、功耗)
- 使用定点数 - 有效降低浮点数运算开销
- 架构设计要一定灵活性,尽量兼容比较多的 NeRF 衍生网络
如何使用定点数?
目前的实现是将在 GPU 上训练好的 NeRF 的权重进行量化 (quantization),再导出。不过,目前也有一些工作在 quantization-aware training 方面,可能对这个网络的训练过程有所帮助。
位置编码单元 (PEU)
设计位置编码单元 (Positional Encoding Unit, PEU) 的目的是在 PEU 前和 PEU 后的向量维数增加了很多倍(对原 NeRF 来说位置是 20 倍,方向是 8 倍),如果在 ICARUS 内部进行计算的话,可以减少很大一部分外部存储传输,降低传输总用时。
PEU 部件主要在做这件事:
$$ \phi(x; A) = [\cos A^T x, \sin A^T x] $$其中 $ A $ 一般为一个行数比列数多的矩阵,用来升维。
PEU 单元对应的设计如下 (Fig. 4(b)):
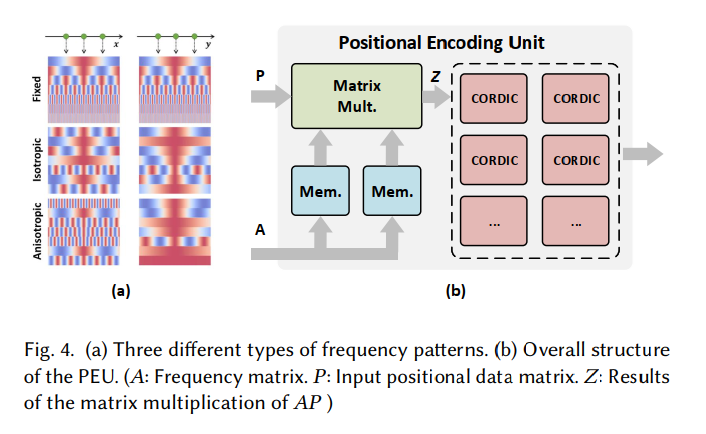
可以看到,就是矩阵乘法单元和 CORDIC 单元的组合。
一些关于矩阵乘和 CORDIC 单元的大概印象:
矩阵乘:有很多工作,比如搜索 Systolic array 等等
- 不过我不清楚 SOTA 情况
CORDIC: https://zipcpu.com/dsp/2017/08/30/cordic.html- 不过我也不清楚 SOTA 情况
具体设计上来说,ICARUS 支持对 dim=3 和 dim=6 的两种输入进行位置编码,并且扩展到 dim=128。PEU 内部设计有两个 3x128 的内存块和 6 组 MAC (Multiply-ACcumulate) 单元,当计算 dim=6 的输入时会全部启用,当计算 dim=3 的输入时只启用一半。
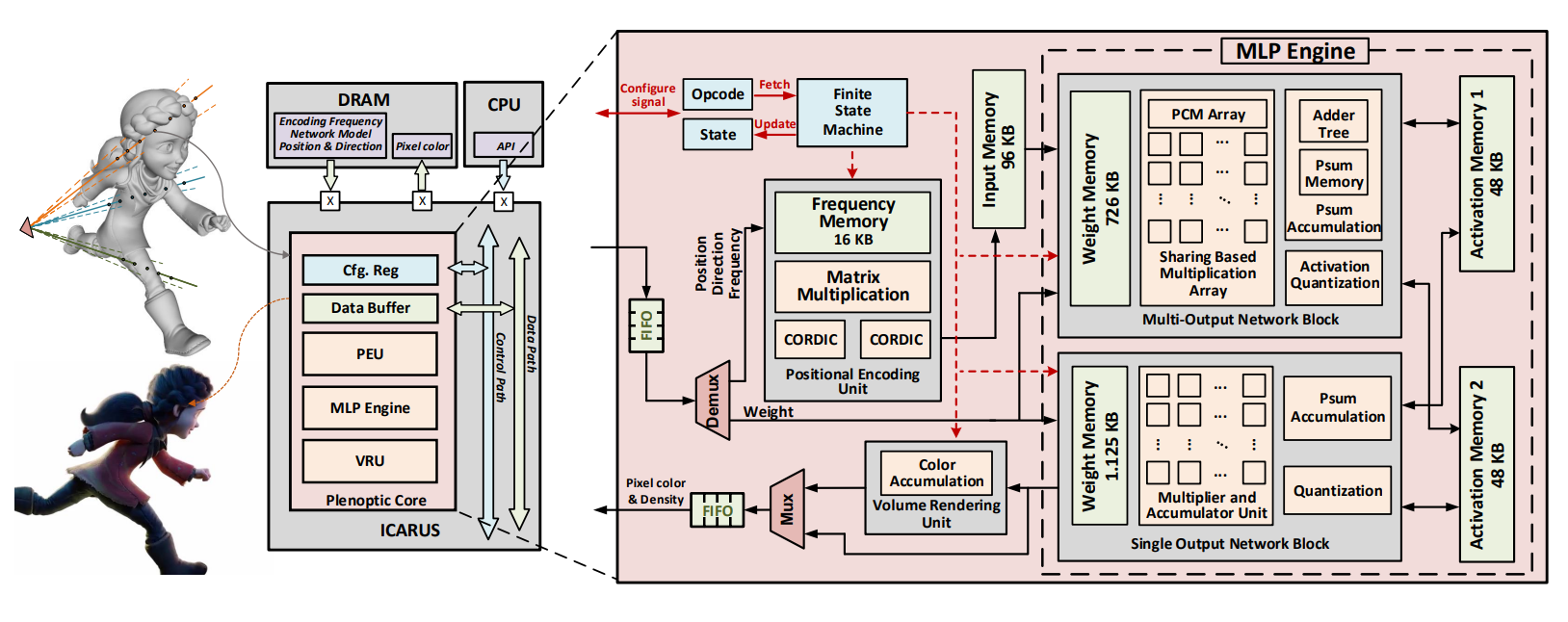
MLP Engine
MLP 引擎主要进行 $ f(Wx+b) $ 类型的计算。
MLP 引擎包含有:
- 一个 Multi-output Network block (MONB),负责计算中间的隐藏层
- 一个 Single-output network block (SONB),负责计算最后的输出层
- 不继续用 MONB 的原因是,全连接的 MONB 比只输出一个数字的 SONB 面积要大得多
- 两个 activation memory block
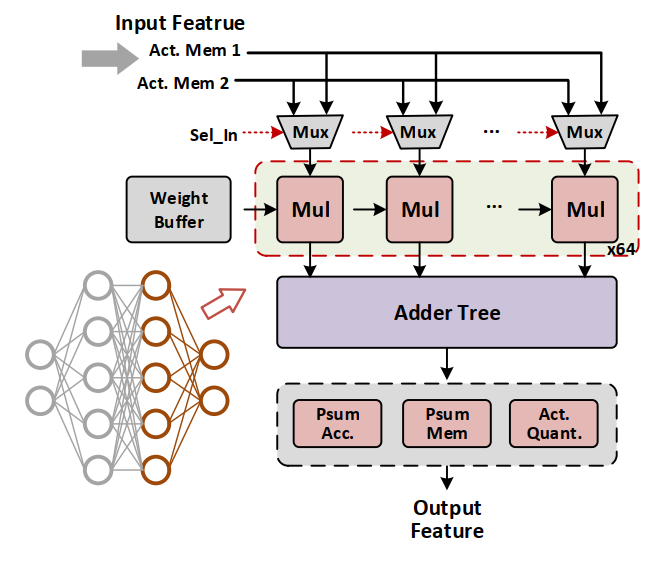
对于 MLP 计算来说,实现是这样的:
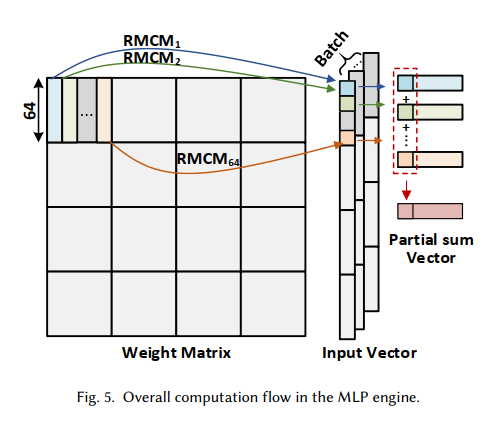
首先,将 MLP 的权重拆成 64 x 64 的小块,方便硬件上的复用,并且同样的权重可以被多组输入向量复用,从而降低内存带宽开销,代价方面只需要暂存该 batch 内的中间结果就可以(这里选择 batch_size=128)。
每个 64 x 64 的矩阵-向量乘法再进行分片,变成按矩阵列分割的 64 个列向量 - 向量的内积乘法(即 $ [\alpha_1 … \alpha_{64}] [x_1 … x_{64}]^T $,每个 $ \alpha_i x_i $ 的部分和用一个 RMCM 模块实现:
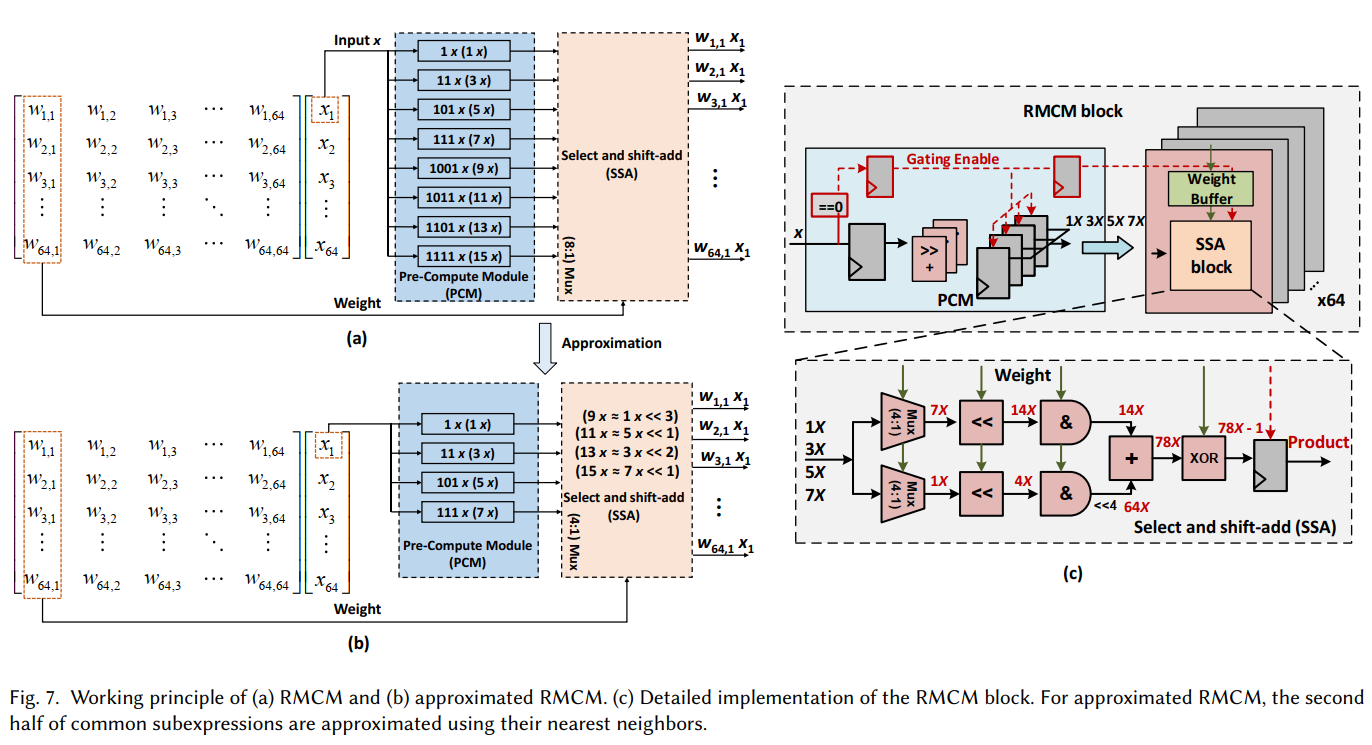
大概来说,是因为乘法可以变成移位加法:
$$ 3x = 1x << 1 + 1x $$所以权重 load 进来的作用就是预先选择好路径上的移位和加法器,然后数据从这些器件中流过去就行。
另一个优化是高一半的移位和加法路径直接用上一次的值来替换,然后网络训练的时候也作此改动。这样可以节省 1/3 的面积,同时输出基本没有视觉质量损失。
SONB 的架构基本上和 MONB 差不多,只是 RMCM 块用不到了,用普通的向量乘法块就可以了。
Volume Rendering Unit
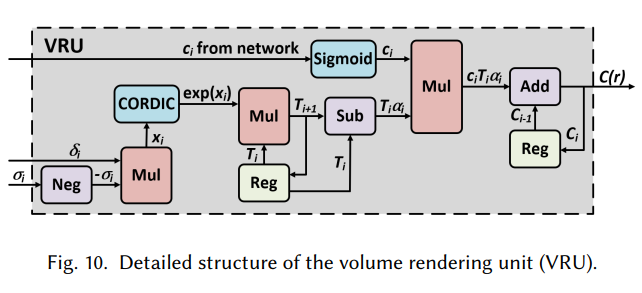
VRU 模块主要要负责下面的计算:
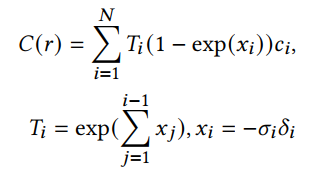
这里,他处理成下面的形式:
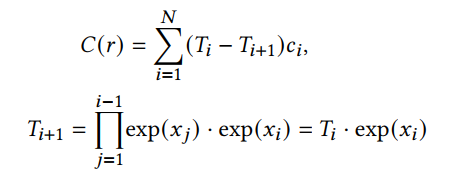
然后用上面的网络计算。
原型验证
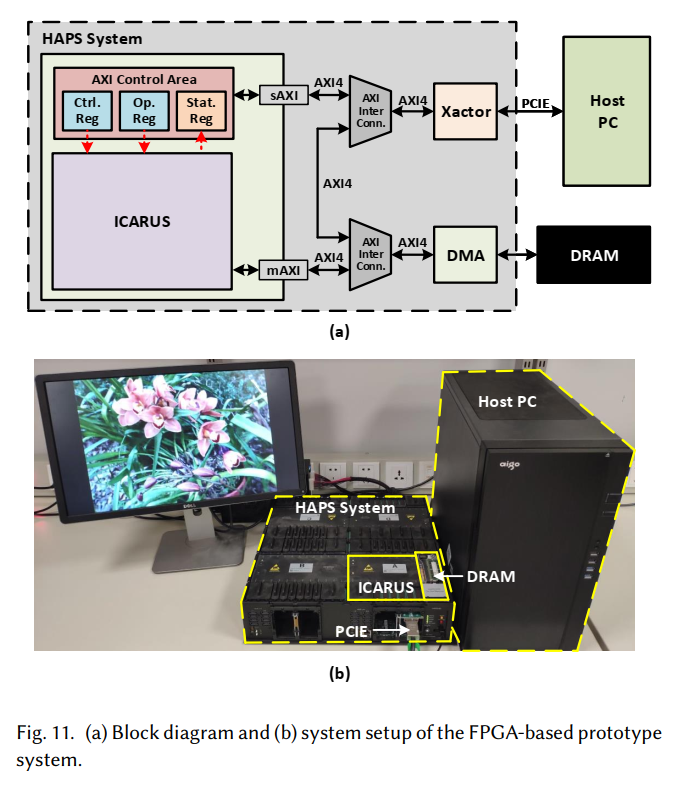
验证平台使用的是 Synopsys HAPS-80 S104,验证时使用的工艺是 40nm CMOS 工艺。